Dieses Praktikumsprotokoll entstand während meines Physikstudiums im Rahmen des Moduls C-Praktikum. Es wurde von meinem Praktikumspartner und mir erstellt, wobei mein Kommilitone nicht namentlich genannt werden möchte. Das Protokoll wurde zwar testiert, es können sich allerdings dennoch inhaltliche oder grammatikalische Fehler darin befinden. Sollte jemand solche Fehler finden, wäre ich froh wenn er sie mir mitteilt.
Optische Spektroskopie
Inhaltsverzeichnis
1.2. Brechung, Reflexion und elektromagnetische Wellen
1.3. Totalreflexion und Glasfaser-Lichtleiter
1.4. Schwarzer Körper und Plancksches Strahlungsgesetz
1.5 .Glüh-, Leuchtstoff- und Halogenglühlampe
1.8. Gitterspektrometer und Interferenzen
2.2. Anteil des sichtbaren Lichts von einer Quecksilber-Dampflampe und Energiesparlampe
Abbildung 1: Spektrum einer Glühbirne
Abbildung 2: Intensität über Wellenlänge Messung 1
Abbildung 3: Intensität über Wellenlänge Messung 2
Abbildung 4: Intensität über Wellenlänge Messung 3
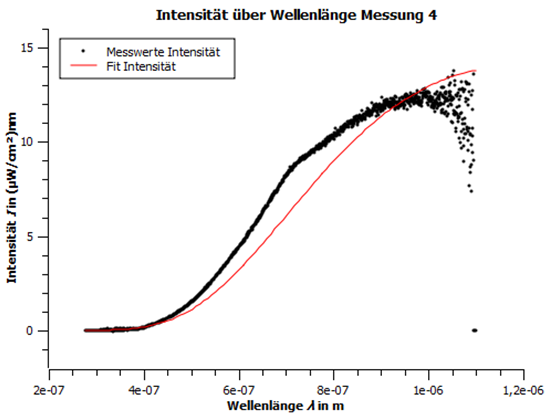
Abbildung 5: Intensität über Wellenlänge Messung 4
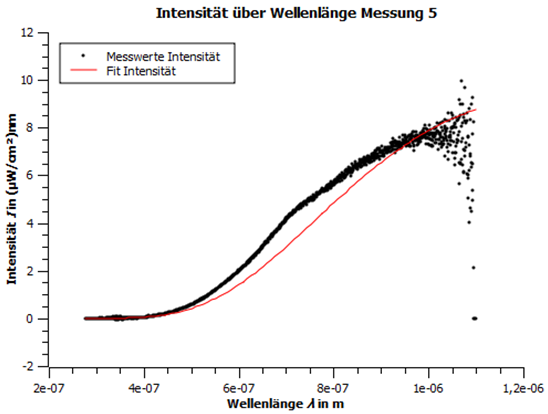
Abbildung 6: Intensität über Wellenlänge Messung 5
Abbildung 7: Intensität über Wellenlänge Messung 6
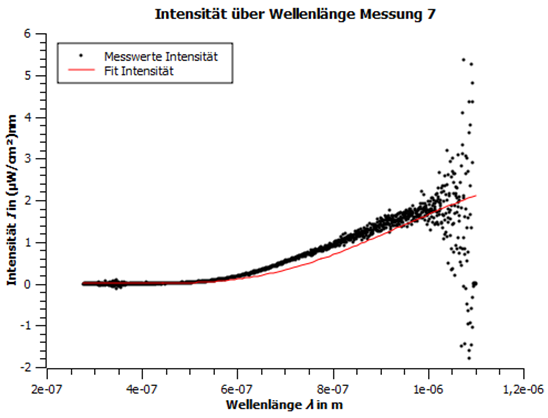
Abbildung 8: Intensität über Wellenlänge Messung 7
Abbildung 9: Intensität über Wellenlänge Fits
Abbildung 10: Maximale Wellenlänge von T
Abbildung 11: Spektrum einer Quecksilber-Dampflampe
Abbildung 12: Spektrum einer Energiesparlampe
Abbildung 13: Spektrum der Energiesparlampe
Abbildung 14: Spektrum der Hg-Lampe
Abbildung 15: Spektrum einer LED-Lampe
Das Ziel dieses Versuches ist es sich mit verschiedenen künstlichen Lichtquellen und ihren Lichtspektren auseinander zu setzen. Weiterhin dient der Versuch dazu, sich mit dem schwarzen Körper vertraut zu machen und seine Abstrahlung mit der von Glühlampen zu vergleichen.
1.2. Brechung, Reflexion und elektromagnetische Wellen
Wenn Licht auf eine Grenzfläche zwischen zwei Medien mit verschiedenen Brechungszahlen auftrifft, dann wird in den meisten Fällen ein bestimmter Teil des Lichtes reflektiert. Dabei entspricht der Reflexionswinkel dem Einfallswinkel. Der Grund dafür ist, dass die Atomelektronen innerhalb des Mediums durch die Welle des ankommenden Lichtes zum Schwingen gezwungen werden. Dabei wirken sie als schwingende Dipole, weswegen sie dann selbst wiederelektromagnetische Wellen mit der Erregerwellenfrequenz ausstrahlen. Allerdings erfährt dabei die Phase der erzwungenen Schwingung eine Verzögerung gegenüber der Phase der Erregerschwingung. Dies gilt ebenfalls für das Gesamtwellenfeld, da sich dieses aus den beiden Wellen zusammensetzt. Deswegen verändert sich im zweiten Medium auch die Geschwindigkeit des Lichtes. Diese Änderung kann mit der Gleichung:
(1.2.1)
bestimmt werden, wobei c der Lichtgeschwindigkeit im Vakuum, n dem Brechungsindex des Mediums und der Lichtgeschwindigkeit innerhalb dieses Mediums entspricht. Da bei der Brechung sich die Frequenz f nicht ändert, entspricht nun die Wellenlänge des Lichts, welches einfällt, nicht mehr der Wellenlange des transmittierten Lichts. Deshalb gilt nun:
(1.2.2)
(1.2.3)
woraus folgt:
(1.2.4)
Es gilt weiterhin, dass die Stärke der Brechung ist umso größer, desto größer der Einfallswinkel des Lichtes ist. Dabei gilt das Snelliussche Brechungsgesetz:
(1.2.5)
wobei der Einfallswinkel, der Brechungswinkel, der Brechungsindex im Bereich des einfallenden Strahls und der Brechungsindex im Bereich des transmittierten Strahls ist. Dabei werden die Winkel normalerweise zwischen Licht und dem Lot auf die Grenzfläche gemessen. Wenn ein Übergang in ein Medium mit geringerem Brechungsindex stattfindet, dann ändert sich die Ausbreitungsrichtung vom Lot weg und bei einem Übergang in ein Medium mit höherem Brechungsindex zum Lot hin. Der restliche Teil des Lichts hingegen dringt durch die Grenzfläche, man nennt diesen Vorgang auch transmittieren, und wird dabei normalerweise gebrochen. Weiterhin besteht beim Transmittieren die Möglichkeit, dass ein Teil der Intensität verloren geht, dies wird auch als Absorption bezeichnet. Außerdem existieren auch elektromagnetische Wellen, ein Beispiel hierfür wäre Licht, welche eine transversale elektromagnetische Welle ist. Dabei stehen ihre elektrischen und magnetischen Feldstärkevektoren senkrecht sowohl aufeinander als auch auf der Ausbreitungsrichtung. Wobei die Polarisationsebene dem magnetischen Feldstärkevektor zugeordnet wird und die sogenannte Schwingungsebene dem elektrischen Feldvektor . Dabei kann die Polarisation einer elektromagnetischen Welle genau bestimmt werden und zwar mittels der Gleichung:
(1.2.6)
dabei handelt es sich bei um die Kreisfrequenz, t um die Zeit, k um den Wellenvektor, r um den Ort und um die Amplitude. Wenn man jetzt beispielsweise die Wellenausbreitung in Richtung der z-Achse betrachtet, dann findet dabei die Schwingung des Feldvektors nur in einer einzigen Ebene statt. Wenn nun die Wellenkomponente x und y in Phase schwingen, dann handelt es sich um linear polarisiertes Licht und wenn die beiden Komponenten den gleichen Betrag haben:
(1.2.7)
dann existiert eine 90° Phasenverschiebung und es gilt:
(1.2.8)
(1.2.9)
Dadurch wird eine, sich um die z-Achse bewegende, Kreisspirale durch beschrieben, was man auch als zirkular polarisiertes Licht bezeichnet. Außerdem existiert noch elliptisch polarisiertes Licht, welches dann auftritt, wenn:
(1.2.10)
gilt und deswegen eine Phasenverschiebung vorliegt, welche nicht um 90° verschoben ist.
1.3. Totalreflexion und Glasfaser-Lichtleiter
Ein Sonderfall der Brechung ist die Totalreflexion, bei dem fast ausschließlich reflektiertes Licht und kein transmittiertes entsteht, also kein Übergang in das zweite Medium mehr stattfindet. Dieser Vorgang findet nur an der Grenzfläche von nicht absorbierenden Medien statt, welche über unterschiedliche große Ausbreitungsgeschwindigkeiten verfügen. Außerdem muss der Einfallswinkel größer als der Grenzwinkel der Totalreflexion, welcher auch als kritische Winkel bezeichnet wird, sein. Ermittelt wird der kritische Winkel durch das Snelliussche Brechungsgesetz:
(1.3.1)
Wenn nun der Einfallswinkel größer als der kritische Winkel wird, so muss er nach dieser Gleichung auch größer als 90° werden. Dadurch ist es dem Lichtstrahl nun nicht mehr möglich in das zweite Medium überzugehen und wird dadurch, zumindest bei transparenten Materialien, vollständig reflektiert, wobei der Ausfallswinkel weiterhin dem Einfallswinkel entspricht. Diese Tatsache wird bei den so genannten Lichtwellenleitern ausgenutzt, um beispielsweiße digitale Daten schnell und über große Entfernung effizient zu übermitteln. Diese bestehen aus vielen Quarzglas- oder Kunststofffasern, welche normalerweise zu ihrem Schutz noch mechanisch verstärkt sind. Dabei liegen die lichtführenden Fasern im Inneren der Kabel und haben einen Gesamtdurchmesser zwischen einigen Mikrometern bis hin zu einigen Millimetern. Umgeben sind sie dann mit einem Mantel, welcher einen niedrigeren Brechungsindex als die Fasern hat. Dieser besteht meistens aus reinem Quarzglas, dass mit verschiedenen Zusätzen, wie Bor oder Fluor, dotiert wird. Um den Mantel herum befindet sich dann noch eine Schutzbeschichtung und Schutzhülle, um so die Beschädigung des Kabels zu verhindern. Wird nun eine elektromagnetische Strahlung in das Kabel gesendet, dann erfolgt zwischen den Fasern im Inneren und dem Mantel eine Lichtbrechung, welche zur bereits beschriebenen Totalreflexion führt und die Strahlung so verlustfrei übertragen kann.
1.4. Schwarzer Körper und Plancksches Strahlungsgesetz
Ein schwarzer Körper, auch schwarzer oder planckscher Strahler genannt, ist eine idealisierte thermische Strahlungsquelle. Seine Funktion ist das vollständige und ausschließliche Absorbieren jeglicher elektromagnetischer Strahlung, unabhängig von ihrer Wellenlänge, welche auf seiner Oberfläche auftrifft. Anschließend erfolgt ein Aussenden der vorher absorbierten Energie, deren Spektrum nun aber ausschließlich von der Temperatur abhängig ist. Die Frequenzverteilung und Intensität der vom schwarzen Körper ausgesendeten Energie kann durch das plancksche Strahlungsgesetz beschriebene werden:
(1.4.1)
wobei h für das plansche Wirkungsquant, für die Boltzmann-Konstante und T für die Temperatur steht. Hergeleitet wird das Gesetz durch die Gleichung:
(1.4.2)
Diese Gleichung basiert auf der Schwingung, welche die Elektronen auf der Oberfläche des schwarzen Körpers mit einer bestimmten Frequenz durchführen, und auf der dadurch entstehenden Wellenbewegung mit der gleichen Frequenz. Nach der Maxwellschen elektrodynamischen Theorie zwischen der Energie eines linearen Oszillators, welcher eine elektromagnetische Welle mit einer Frequenz f bis erzeugt, und dem spektralen Emissionsvermögen entsteht nun die Formel (1.4.2). Weiterhin lässt sich auch darstellen wie die Gleichung:
(1.4.3)
Erkannt wurde dies durch Planck, welcher feststellte, dass die Übereinstimmung mit den Ergebnissen des Experimentes nur dann gegeben ist, wenn man für die mittlere Energie der Oszillatoren die Formel (1.4.3) einsetzt. Wenn man dies allerdings nicht tut, so wird das theoretisch ermittelte Emissionsvermögen bei sehr kleinen Wellenlängen gegen unendlich gehen, was dem experimentell gemessenen Emissionsvermögen wiederspricht. Fügt man nun also (1.4.3) in (1.4.2) ein, so erhält man schließlich (1.4.1). Das Strahlungsgesetz spielt weiterhin auch eine Rolle bei der Bestimmung der maximalen Energie von strahlenden Körpern, beispielsweiße der Sonne. Es verdeutlicht auch, dass bei sehr hohen Temperaturen eine Verschiebung der Maxima von spektralen Emissionen zu kürzeren Wellenlängen erfolgt. Des Weiteren verschiebt sich bei steigender Temperatur auch das Maximum der Frequenzverteilung und damit direkt zu höheren Frequenzen und niedrigeren Wellenlängen. Dies wird durch das Wiensche Strahlungsgesetz, wie folgt, beschrieben:
(1.4.4)
dabei steht für die absolute Temperatur und für die maximale Intensität für ein Wellenlängenintervall. Ebenfalls noch zu erwähnen, ist plancksche Strahlungsspektrum eines Schwarzen Körpers bei unterschiedlichen Temperaturen. Es sind dabei deutlich die jeweiligen Strahlungsmaxima zu erkennen, der schnelle Abfall bei kleinen Wellenlängen und ein wesentlich langsamerer Abfall bei Größeren. Dabei erfolgt eine Verschiebung der Maxima in Richtung kleinerer Wellenlängen wenn die Temperatur zunimmt, genau wie es vom Wiensche Verschiebungsgesetz verlang wird. Des Weiteren erfolgt eine Zunahme der Strahlungsleistung P, gemäß dem Stefan-Boltzmann-Gesetz:
(1.4.5)
wobei für die Stefan-Boltzmann-Konstante und A für die Fläche steht. Die Stefan-Boltzmann-Konstante ist dabei wie folgt definiert:
(1.4.6)
Durch dieses extreme Ansteigen der Strahlungsintensität bei höheren Temperaturen, erklärt auch die immer größer werdende Bedeutung der Wärmeabstrahlung. Weiterhin existiert die spektrale spezifische Ausstrahlung für einen Schwarzen Körper mit der absoluten Temperatur T, welche in der Wellenlängendarstellung wie folgt aussieht:
(1.4.7)
dabei entspricht der Intensität.
1.5. Glüh-, Leuchtstoff- und Halogenglühlampe
Die Glühlampe ist eine künstliche Lichtquelle, welche durch elektrischen Strom zum Leuchten gebracht wird. Dazu wird als Erstes ein Strom durch einen dünnen, leitenden Draht, aufgrund der hohen Hitzebeständigkeit meistens Wolfram, geschickt. Dadurch wird der Draht, je nach Modell, auf 1000°C bis 4000°C erhitzt. Dies sorgt dafür dass der Draht beginnt zu glühen und deswegen anfängt elektromagnetische Strahlung auszusenden, welche größtenteils im Bereich des sichtbaren und infraroten Lichtes liegt. Allerdings wird von der aufgenommenen elektrischen Leistung nur etwa 5% in sichtbares Licht umgewandelt, während der Rest in Infrarotlicht und Wärme umgewandelt wird. Außerdem ist der Draht von einem Glaskolben umgeben um ihn von der Umgebungsluft abzuschirmen, das er sonst wegen dem Sauerstoff und der hohen Temperatur sehr schnell zu Wolframoxid verbrennen würde. Dabei ist die Größe des Kolbens abhängig von der Sublimationsrate des verwendeten Drahtmaterials und damit umso größer je höher die Leistung der Glühlampe ist. Dadurch wird verhindert, dass das sublimierte Material zu schnell die Kolbeninnenfläche bedeckt und damit die Ausstrahlung des Lichts behindert. Um die Sublimation und Wärmeleitung zusätzlich noch weiter zu verringern, befindet sich innerhalb des Kolbens ein Schutzgas, meistens eins Stickstoff-Argon-Gemisch. Eine Halogenglühlampe funktioniert ähnlich wie eine herkömmliche Glühlampe, allerdings wird ihr noch zusätzlich das Halogen Iod, alternativ auch Brom, zugegeben. Das hinzugefügt Iod reagiert nun mit den Wolframatomen, welche durch den Glühdraht verdampft werden, wodurch eine stabile und wolframhaltige Atmosphäre erzeugt wird. Außerdem verhindert das Halogen, dass sich das Wolfram bei Temperaturen über 250 °C auf den Glaskolben niederschlägt. Dies ermöglicht es den Kolben kleiner zu gestalten und einen höheren Betriebsdruck zu verwenden, als bei normalen Glühlampen. Durch den höheren Druck reduziert sich dann die Abdampfrate des Drahtes, wodurch bei Betriebstemperaturen von 2800 K bis 3100 K eine längere Lebensdauer und eine leicht höhere Lichtausbeute erreicht wird. Die Lichtausbeute kann durch eine Steigerung der Leistungsaufnahme auf über ein kW noch deutlich verbessert werden, allerdings reduziert sich dabei die Betriebsdauer auf wenige Stunden. Weiterhin zerfällt die Verbindung zwischen den beiden Stoffen bei zu hohen Temperaturen wieder und die Wolframatome schlagen sich an den kältesten Drahtstellen nieder, der gesamte Prozess ist also reversibel.
Die Gasentladungslampe ist eine mit Gas gefüllte Röhre, in der sich eine Anode und Kathode befindet. Durch das Anlegen eine röhrenspezifischen Mindestspannung kommt es zu einer Gasentladung innerhalb der Röhre und damit zum einem Aussenden von Licht. Je nachdem ob es sich um ein Niederdruck-, Hoch- oder Höchstdrucklampe handelt, herrschen unterschiedlich starke Drücke und die Röhre besteht entweder aus normalem Glas, Quarzglas oder Aluminiumoxid-Keramik. Bei der Leuchtstofflampe handelt es sich um eine Niederdrucklampe, welche mit Quecksilberdampf und meistens noch zusätzlich mit Argon gefüllt ist. Zusätzlich ist die Röhre in ihrem Inneren mit einem Leuchtstoff beschichtet. Durch das Anlegen einer hohen Zündspannung, erfolgt die Ionisierung der Gasfüllung wodurch sie elektrisch leitend wird und sich ein Plasma bildet. Dieses bleibt so lange erhalten bis die Mindestspannung, welche vom Druck des Gases abhängig ist, unterschritten wird. Wenn nun die beschleunigten Elektronen die Quecksilberatome anregen und diese anschließend wieder auf ein niedrigeres Energieniveau zurück fallen, dann strahlt das Plasma ultraviolette Strahlung aus. Trifft sie nun auf den fluoreszierenden Leuchtstoff, beginnt diese zu leuchten und wandelt so die kaum sichtbare ultraviolette Strahlung in sichtbares Fluoreszenzlicht um. Die Quecksilberdampflampe enthält, genau wie die Leuchtstofflampe, Quecksilber allerdings immer noch ein zusätzliches Edelgas, ansonsten ist die Funktionsweiße mit der der Leuchtstofflampe identisch. Allerdings unterscheiden sich die Anwendungsbereiche, da bei der Quecksilberdampflampe meistens kein Leuchtstoff verwendet wird. Stattdessen wird die von ihr erzeugte UV-Strahlung genutzt, um beispielsweiße die Aushärtung bestimmter Lacke zu beschleunigen, für die Fotolithografie in der Halbleitertechnik oder für die Atomspektroskopie. Außerdem werden sie für die Straßenbeleuchtung verwendet, dabei allerdings als Hochdrucklampen, mit einem Arbeitsdruck von rund zehn bar, welcher durch die Erhitzung erreicht wird. Dies sorgt für eine bessere Lichtausbeute und sie nehmen dabei eine blaugrüne Lichtfarbe an. Allerdings geben sie erst dann viel Licht ab, wenn eine bestimmte Menge an Quecksilber verdampft ist. Die Natriumdampflampe ist ebenfalls eine Gasentladungslampe und funktioniert im Prinzip wie eine Quecksilberdampflampe, enthält allerdings kein Quecksilber sondern Natrium. Dadurch fällt auch der fluoreszierende Leuchtstoff weg, da hier die Gasentladung selbst schon Licht produziert, welches im für den Menschen sichtbaren Bereich liegt. Sie gehört weiterhin mit zu den effizientesten elektrischen Lichtquellen, verfügt über eine hohe Lebensdauer und wird häufig für die Straßenbeleuchtung eingesetzt.
Die Leuchtdiode, auch light emitting diode oder kurz LED genannt, ist ein Halbleiter-Bauelement, ähnlich einer Diode, welches Licht aussendet. Sie besteht aus einem n-leitenden Grundhalbleiter auf dem sich dann eine äußerst dünne p-leitende Halbleiterschicht befindet, welche über eine große Löcherdichte verfügt und aufgrund ihrer geringen Dicke lichtdurchlässig ist. Nun erfolgt eine Überschwemmung der LED Grenzschicht mit freien Ladungsträgern, welche, aufgrund der Polung in Durchlassrichtung, zu einer Rekombinierung der Elektronen mit den Löchern führt. Dadurch beginnen die Elektronen Energie abzugeben, was als Lichtblitze wahrgenommen wird. Aufgrund der Lichtdurchlässigkeit können die Lichtblitze nun die p-leitende Halbleiterschicht durchdringen. Dabei ist die Intensität der Lichtblitze und damit die Helligkeit des Lichts abhängig von der Stromstärke. Da der Halbleiterkristall selbst nur über eine sehr geringe Lichtabstrahlung verfügt, wird das Material unterhalb des Kristalls in Halbkugelform gebracht, wodurch ein Streuen des Lichts stattfindet. Das umgebende Gehäuse der LED wird dann wie eine Linse konstruiert und bündelt dadurch dann das Licht. Dies führt dann auch dazu, dass die LEDs in der Lage sind mit bereits wenigen Milliampere eine hohe Lichtabstrahlung zu erreichen. Weitere Vorteile von Leuchtdioden sind die vielen Lichtfarbenspektren, welche sie darstellen können, die geringe Hitzeentwicklung und das Fehlen von UV- und IR-Strahlung. Sie sind aber nicht wasserbeständig und müssen deswegen vor Flüssigkeiten geschützt werden. Aufgrund ihrer vielen Vorteile verfügen sie über einen breiten Einsatzbereich, welcher unter anderem die Innen- und Außenbeleuchtung, die Sensorik und die Displaytechnologie umfasst.
1.8. Gitterspektrometer und Interferenzen
Um die Intensitätsverteilung von elektromagnetischen Strahlungsquellen zu messen, wird das Gitterspektrometer, auch als Gittermonochromator bezeichnet, verwendet. Um die Verteilung zu messen, lässt man als erstes die zu untersuchende Strahlung durch den Eingangsspalt fallen. Nachdem sie dann den Spalt passiert hat, fällt sie auf einen konkaven Spiegel und es entsteht ein paralleler Strahl, welcher in Richtung Gitter reflektiert wird. Das Gitter zerlegt nun den Strahl in einzelne Wellenlängen und reflektiert sie anschließen zum zweiten Spiegel. Dieser bündelt nun, in der Brennebene, den zerlegten Strahl und schickt ihn anschließen zum Ausgangsspalt. Die nun austretende Wellenlänge wird mittels eines Strahlungsdetektors, meistens ein Sekundärelektronenvervielfacher, gemessen. Weiterhin kann der Aufbau des Spektrometers je nach Anwendungsfall leicht variieren, beispielsweiße können statt konkaven Spiegel auch entsprechende Linsen verwendet werden. Außerdem besteht das Gitter, welche die Strahlung zerlegt, aus vielen spaltartigen Öffnungen, die mit einem kleinen Abstand voneinander angeordnet sind. Diese sorgen nun dafür, dass eine einfallende Welle sich in zwei kreisförmige, von den Öffnungen aus verlaufende, Wellen aufspaltet. Diese beiden Wellen überlagern sich nun an bestimmten Positionen, wodurch es zu konstruktiver und zu destruktiver Interferenz kommt. Dabei tritt konstruktive Interferenz dann auf, wenn der Gangunterschied der beiden Wellen ein ganzzahliges Vielfaches der Wellenlänge ist. Dadurch trifft also immer ein Wellental auf ein anderes Wellental und jeder Wellenberg ebenfalls auf einen anderen. Verfügen sie dabei über dieselbe Amplitude, führt die Interferenz zu einer Verdoppelung der Amplitude. Beträgt der Gangunterschied allerdings nur ein Vielfaches der halben Wellenlänge, so trifft immer ein Wellental auf einen Wellenberg und umgekehrt. Daraus resultiert immer eine Welle, welche kleiner ist als die Ausgangswellen, weswegen man dies dann destruktive Interferenz nennt. Haben in diesem Fall die Wellen dieselbe Amplitude, so führt dies zu einer vollständigen Auslöschung der Wellen.
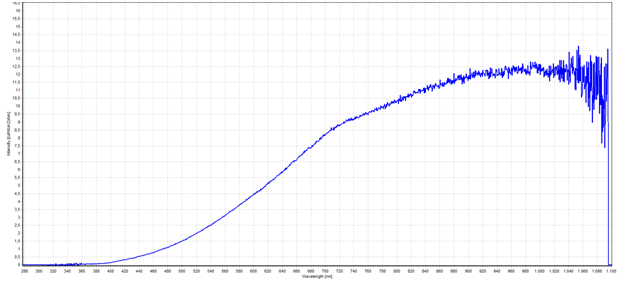
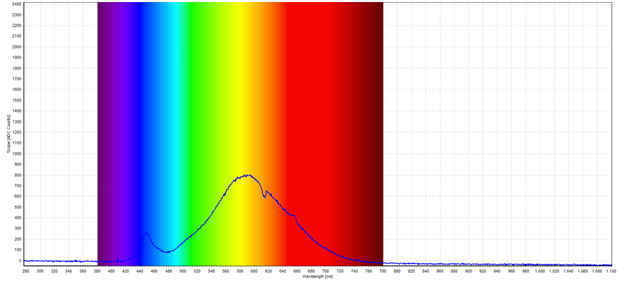
Im ersten Versuchsteil wurde eine Glühbirne über einen Dimmer angeschlossen und anschließend für verschiedene Spannungen das Spektrum der Glühbirne über ein Spektrometer am Computer aufgenommen. Abbildung 7 zeigt beispielhaft eines der aufgenommenen Spektren.
Abbildung 1: Spektrum einer Glühbirne
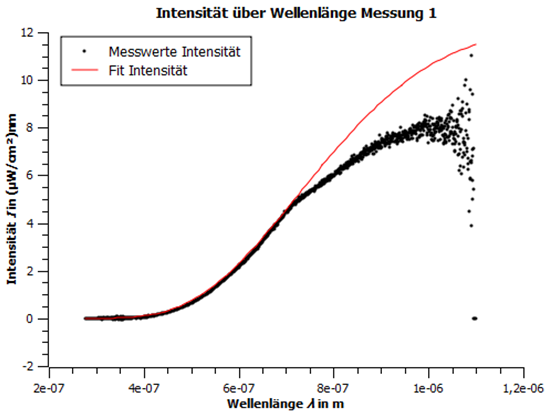
Es wurden auch die Farbtemperaturen gemessen und mit diesen als Startwerte in SciDAVis die gemessenen Intensitätswerte an das plancksche Strahlungsgesetz angefittet. Die Messwerte der Intensität über der Wellenlänge sowie die dazugehörigen Fits sind in den folgenden Abbildungen zu sehen.
Abbildung 2: Intensität über Wellenlänge Messung 1
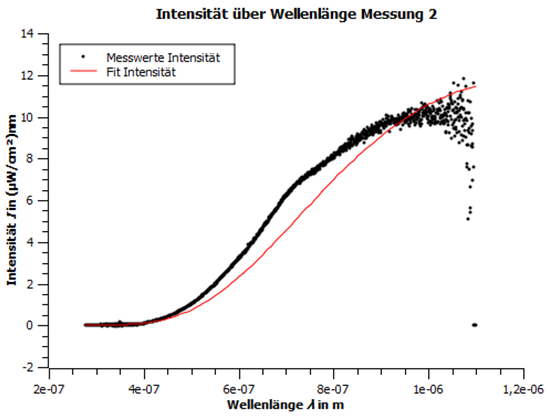
Abbildung 3: Intensität über Wellenlänge Messung 2
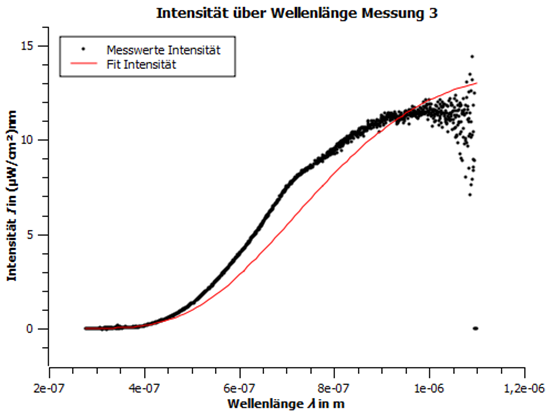
Abbildung 4: Intensität über Wellenlänge Messung 3
Abbildung 5: Intensität über Wellenlänge Messung 4
Abbildung 6: Intensität über Wellenlänge Messung 5
Abbildung 7: Intensität über Wellenlänge Messung 6
Abbildung 8: Intensität über Wellenlänge Messung 7
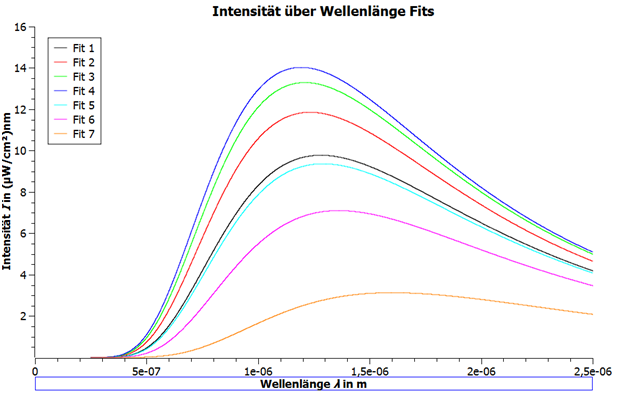
Die Intensitäten wurden nun als Funktionen der Wellenlängen nach dem planckschen Strahlungsgesetz mit den gefitteten Parametern im Bereich bis 2500 nm aufgetragen.
Abbildung 9: Intensität über Wellenlänge Fits
|
T in K |
|
|
1281,38 |
2261,11 |
|
1232,90 |
2349,98 |
|
1209,95 |
2394,34 |
|
1193,07 |
2428,19 |
|
1291,40 |
2243,40 |
|
1361,16 |
2128,29 |
|
1601,71 |
1808,71 |
Tabelle 1: Wellenlänge und Temperatur
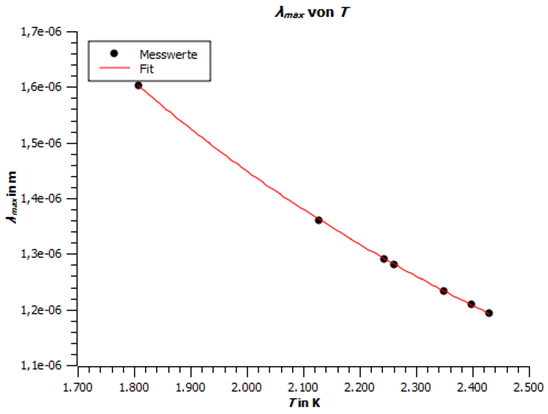
Für die gefitteten Funktionen wurden nun an der maximalen Intensität die dazugehörigen Wellenlängen abgelesen. In Tabelle 1 sind diese Wellenlängen zu finden, zusammen mit der Farbtemperatur der Messung. Nun wurde als Funktion von T aufgetragen und mit einem Parameter b an das Wiensche Verschiebungsgesetz angepasst. Für den Parameter b ergibt sich:
Abbildung 10: Maximale Wellenlänge von T
2.2. Anteil des sichtbaren Lichts von einer Quecksilber-Dampflampe und Energiesparlampe
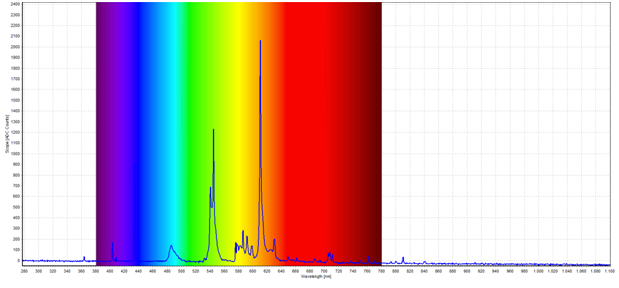
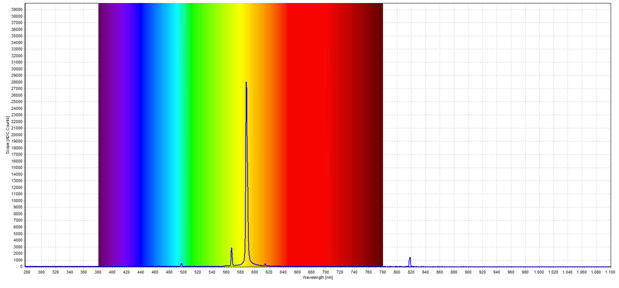
In diesem Versuchsteil wurde das Spektrum einer Quecksilber-Dampflampe und einer Energiesparlampe aufgenommen. Die Abbildungen 11 und 12 zeigen die Spektren der Quecksilber-Dampflampe und der Energiesparlampe, mit Markierung des Wellenlängenbereiches für sichtbares Licht.
Abbildung 11: Spektrum einer Quecksilber-Dampflampe
Abbildung 12: Spektrum einer Energiesparlampe
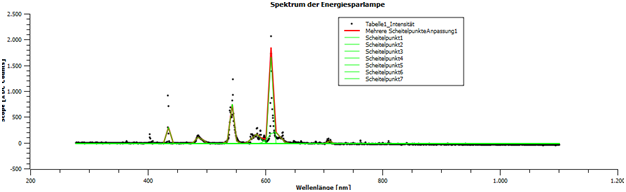
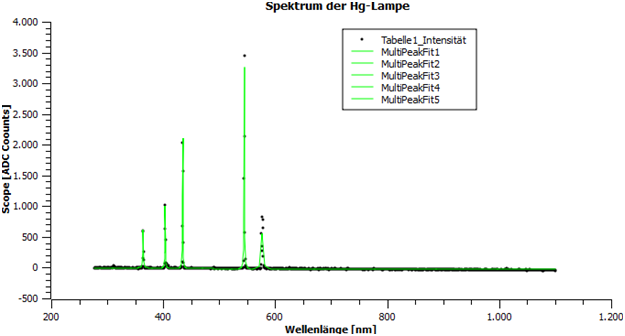
Für beide Spektren wurde nun mit SciDAVis ein Multipeakfit erstellt.
Abbildung 13: Spektrum der Energiesparlampe
Abbildung 14: Spektrum der Hg-Lampe
Anschließend wurde mit der Funktion „Integrieren“ die Fläche unter den Graphen einmal über das gesamte Spektrum und einmal nur über den sichtbaren Bereich von 380 nm bis 780 nm. Dabei ergeben sich die Flächen von
und
und
Der Anteil von sichtbarem Licht im Vergleich zum gesamten abgestrahlten Licht wird berechnet mit und analog dazu.
2.3. Vergleich von anderen Lichtquelle
Im letzten Versuchsteil wurden die Spektren von einer LED-Lampe, eine Na-Lampe und der Deckenlampe des Versuchsraums gemessen. Die Spektren sind in den folgenden Abbildungen zu sehen.
Abbildung 15: Spektrum einer LED-Lampe
Abbildung 16: Spektrum einer Na-Lampe
Abbildung 17: Spektrum der Deckenlampe des Versuchsraumes
Bei der LED-Lampe lässt sich leicht erkennen, dass diese besonders im gelben, sowie blauen Bereich leuchtet. LED-Lampen können kein weißes Licht erzeugen, weshalb dazu die Farben Rot, Blau und Grün gemischt werden, allerdings können auch beliebige andere Farbtöne damit erzeugt werden und bei dieser LED-Lampe wird ein „warmer“ Farbton erzeugt. Die Natriumdampflampe strahlt fast ausschließlich im gelben Bereich, genau wo sich die für Natrium typische Spektrallinie befindet. Sie eignen sich gut als Lichtquellen, falls es nicht nötig ist Farben zu unterscheiden, da sie monochromatisch sind, somit besonders effizient und das menschliche Auge auf diesen Farbbereich besonders empfindlich reagiert. Die Deckenlampe weißt das typische Spektrum von Entladungs-/Leuchtstofflampen auf, welche kein kontinuierliches Spektrum mit Spitzen, in diesem Fall bei Blau, Grün und Orange, besitzen.
Der in diesem Versuch bestimmte Verschiebungsparameter stimmt entspricht unter Berücksichtigung des Fehlers dem Literaturwert [6] der Wien-Konstante . Daraus lässt sich schließen, dass die im Versuch verwendete Glühbirne näherungsweise die Strahlung eines schwarzen Körpers besitzt. Der Anteil des sichtbaren Lichts vom gesamten abgestrahlten Licht scheinen in beiden Fällen nicht richtig zu sein, da bei der Energiesparlampe mehr Licht im sichtbaren Bereich abgestrahlt zu werden scheint, als insgesamt abgestrahlt wird und bei der Quecksilber-Dampflampe scheint das insgesamt abgestrahlte Licht negativ zu sein. Da nur bei den Peaks und nahe daran positive Werte gemessen wurden und fast alle anderen Werte negativ sind, ist zu vermuten, dass das Referenzspektrum nicht richtig eingestellt wurde und die Graphen somit nach unten verschoben waren.
In diesem Versuch wurde die Wien-Konstante bestimmt zu:
und der sichtbare Anteil des abgestrahlten Lichts von der Energiesparlampe und der Quecksilber-Dampflampe zu:
- Bäthe, R., Meyer, O., & Schmidt, M. (3. Juni 2015). Modernus. Abgerufen am 3. Juni 2015 von Modernus: http://modernus.de/led-lampen-leuchten/funktionsweise-einsatzbereiche-a…
- Bockhorst, M. (3. Juni 2015). Energieinfo. Abgerufen am 3. Juni 2015 von Energieinfo: http://www.energieinfo.de/eglossar/leuchtdiode.html
- Demtröder, W. (2009). Experimentalphysik 2 - Elektrizität und Optik (5. überarbeitete und erweiterte Ausg.). Kaiserslautern: Springer-Verlag.
- Eisenhut, C. (6. Mai 2015). Lernort-Mint. Abgerufen am 6. Mai 2015 von Lernort-Mint: http://www.lernort-mint.de/Physik/Optik/lichtberechung_an_grenzen.html
- Forster, M., & Steinbach, S. (12. Juli 2015). Chemgapedia. Abgerufen am 12. Juli 2015 von Chemgapedia: http://www.chemgapedia.de/vsengine/vlu/vsc/de/ch/3/anc/ir_spek/ir_gerae…
- Forster, M., & Steinbach, S. (6. Mai 2015). ChemgaPedia. Abgerufen am 6. Mai 2015 von ChemgaPedia: http://www.chemgapedia.de/vsengine/vlu/vsc/de/ph/14/ep/einfuehrung/well…
- Kuchling, H. (2014). Taschenbuch der Physik (21. Ausg.). München: Carl Hanser Verlag.
- Schnabel, P. (3. Juni 2015). Elektronik Kompendium. Abgerufen am 3. Juni 2015 von Elektronik Kompendium: http://www.elektronik-kompendium.de/sites/bau/0201111.htm
- Tipler, P. A., & Mosca, G. (2009). Physik (6. Ausg.). Springer-Verlag.
- Universität Wien. (3. Juni 2015). Abgerufen am 3. Juni 2015 von Universität Wien: https://www.univie.ac.at/physikwiki/index.php/LV002:LV-Uebersicht/Video…
- Wedler, G., & Freund, H.-J. (2012). Lehrbuch der physikalischen Chemie (6. vollständig überarbeitete und aktualisierte Ausg.). WILEY-VCH Verlag GmbH & Co. KGaA.
- Wikipeda. (3. Juni 2015). Abgerufen am 3. Juni 2015 von Wikipedia: http://de.wikipedia.org/wiki/Gl%C3%BChlampe
- Wikipedia. (3. Juni 2015). Abgerufen am 3. Juni 2015 von Wikipedia: http://de.wikipedia.org/wiki/Schwarzer_K%C3%B6rper
- Wikipedia. (3. Juni 2015). Abgerufen am 3. Juni 2015 von Wikipedia: http://de.wikipedia.org/wiki/Gasentladungsr%C3%B6hre
- Wikipedia. (4. August 2015). Abgerufen am 4. August 2015 von Wikipedia: https://de.wikipedia.org/wiki/Plancksches_Strahlungsgesetz